Distribuzione delle chiusure di mercato

Una domanda che mi sono spesso posto è se le chiusure dei titoli seguano una distribuzione normale. Ho fatto alcune prove per verificare se è corretto assumere un andamento normale. Nello studio ho usato l’indice di borsa FTSMIB, ma ripetendo le prove con diversi titoli sembra che il comportamento sia analogo anche per i diversi titoli.

Il codice è scritto per Jupyter, strumento di analisi abbastanza standard, facie da usare e molto diffuso. Primo importo le librerie.

#Import vari
import yfinance as yf
from datetime import datetime
from datetime import timedelta
import scipy.stats as sp
import pylab
import numpy as np
from matplotlib import pyplot as plt

Poi carico i dati da yahoo, poi li normalizzo attraverso un’operazione, anch’essa comune, logaritmo sui dati, e differenza tra i valori logaritmici.

#carico i dati, uso il FTSEMIB
start = '2015-01-01' 
#ticker = "A2A.MI"
ticker = "FTSEMIB.MI"
sp_list = [ticker]
end = '2020-12-31'
print(f'{ticker} Stock download')
spy = yf.download(sp_list, start,end)

log_spy = np.log(spy.Close)
log_return = (np.diff(log_spy ,axis=0))
spy = spy.iloc[1:,:]
spy.loc[:,('log_return')] = log_return
data = spy.log_return.values

E ora i grafici e l’analisi.

Distribuzione normale

Faccio un fittin dei dati con la curva normale.

xmin, xmax = plt.xlim([-0.2,0.2])
x = np.linspace(xmin, xmax, len(data))
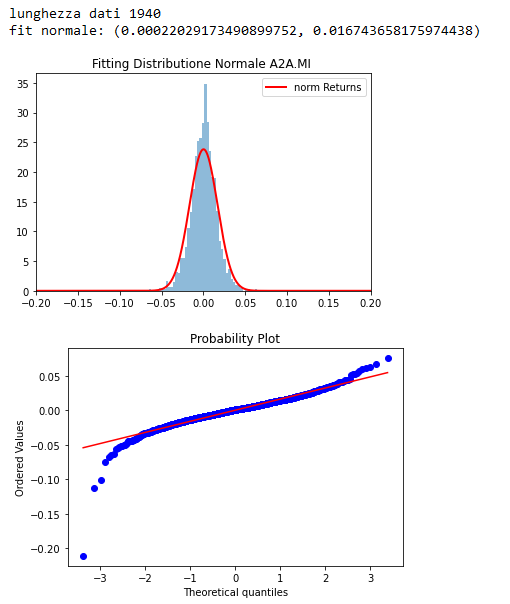
print(f'lunghezza dati {len(data)}')
plt.hist(data, bins=100, density=True, alpha=0.5)

r = sp.norm.fit(data)
print(f'fit normale: {r}')
p1 = sp.norm.pdf( x, r[0], r[1])
plt.plot(x, p1, 'r' ,linewidth=2,label='norm Returns')

# Plot the PDF.
title = f"Fitting Distributione Normale {ticker} " 
plt.title(title)
plt.legend()
plt.show()

sp.probplot(data, dist="norm", plot=pylab)
pylab.show()

Il risultato è quello mostrato in figura, il fitting è solamente discreto, si nota un picco nella parte centrale che supera la curva normale e il grafico delle probabilità conferma che le code sono distanti dai valori della distribuzione normale.

Distribuzione t-Student

Il picco centrale suggerisce che una distribuzione t-student con un basso grado di libertà (< 30) possa avere un fitting migliore.

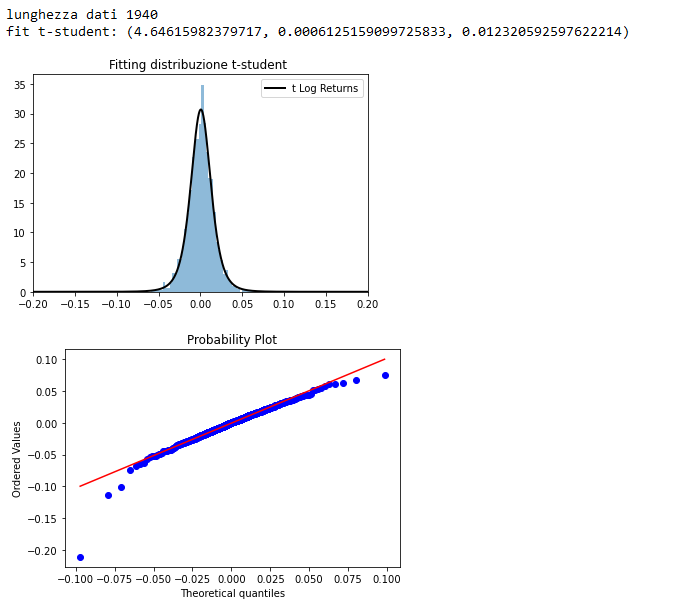
Una distribuzione di t-student sembra in effetti avere un fitting migliore, rimangono delle asimmetrie sulle code e allontanamento dalla norma, con conseguente skewness (asimmetria) e kurtosi.

Approfondimenti da fare: per quali ragioni la distribuzione è t-student?