Tra i diversi indicatori non si trovano spesso indicatori basati sulla regressione lineare, che a mio avviso ha alcuni aspetti interessanti di applicazione.
Dati lineari o logaritmici
La regressione lineare può essere applicata per interpolare i dati di chiusura del mercato e individuare un trend di mercato. L’approccio può essere considerato simile a quelli di una media mobile, con il vantaggio di poter calcolare la pendenza. La prima domanda è se utilizzare i dati lineari o logaritmici. Il dato lineare ha come effetto di essere poco rappresentativo nel momento in cui ci sono grosse variazioni di prezzo. Anche la regressione lineare è sensibile a questa distorsione.
Vediamo a confronto la regressione lineare applicata al medesimo set di dati (TEN ; 2011-10-01 ; 2012-01-01 ) quindi 3 mesi.
I due grafici sono molto simili, ma un occhio attento non sfuggono diverse differenze, come ad esempio l’ultimo gruppo in alto a destra di punti, che risulta molto più vicino alla retta di regressione lineare. Considerando che i titoli possono avere scostamenti considerevoli utilizzerò la regressione lineare su dati esponenziali.
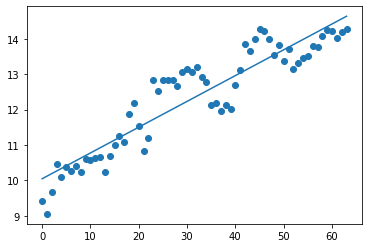
Curva di regressione
Utilizzando la regressione lineare, si può stimare il valore punto successivo della sequenza. Nel caso di scala linerare, il punto futuro è semplicemente y = intercept + slope * (period +1), dove period è il perdo di osservazione del campione. Nel caso di scala logaritmica il punto futuro può essere stimato con y = e ^ intercept * e ^ slope ^ (period +1). Rappresentando graficamente i dati si può verificare la bontà del valore stimato.
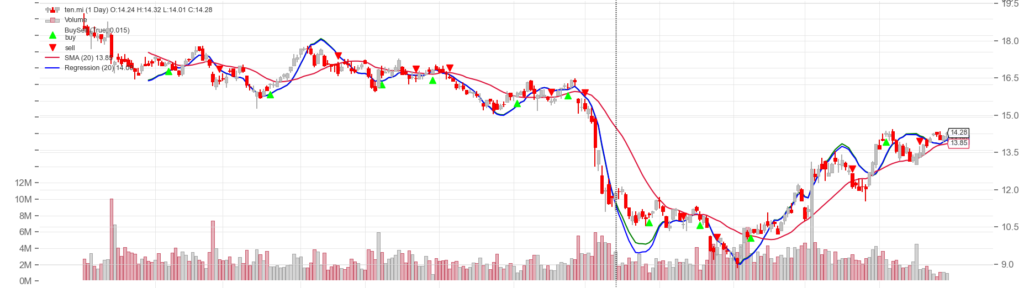
Come per la media mobile, anche la regressione mostra un ritardo (come tutti gli indicatori trend following) , coglie con maggior tempestività il cambio di direzione, ma sembra con un ritardo. L’aspetto interessante è che anche con periodi di osservazione ampi mantiene una buona aderenza con la curva del titolo.
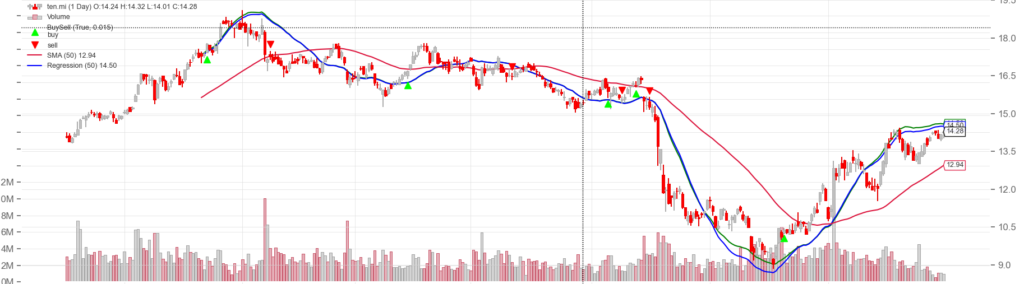
La SMA è decisamente più sensibile all’ampliamento del periodo di osservazione rispetto alla regressione lineare.
Slope/ pendenza ed errore della regressione
La regressione lineare restituisce i seguenti valori: slope, intercept, rvalue, pvalue, sterr = linregress(x, returns). I primi due sono quelli che ho utilizzato per disegnare la curva, il primo stabilisce la pendenza della regressione, il secondo il punto del intercetta sull’asse y. La pendenza della regressione lineare non va confusa con la pendenza della curva rappresenta. Per convertire il coefficiente di pendenza in un incremento % giornaliero occorre tornare nel campo lineare da quello esponenziale. Data la pendenza, ,l’incremento % è dato da % = exp(slope)-1. Il grafico mostra il risultato la curva della pendenza trasformata in %.
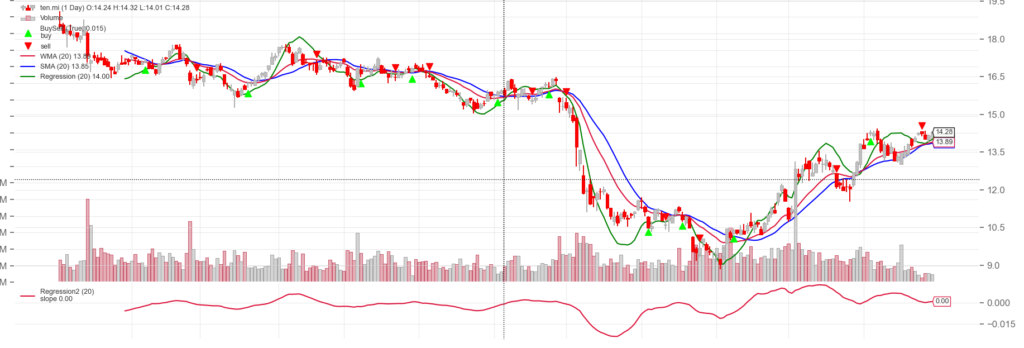
Un aspetto interessante nel grafico soprastante è che WMA, SMA, e REG si intersecano nel punto in cui l’incremento % di REG è pari a 0. Infatti per costruzione quando la pendenza della regressione è pari a 0, il valore successivo è apri all’intercetta, che a sua volta è uguale alla media dei punti, che a sua volta è uguale alla media mobile ponderata. Da osservare che la curva, data dalla formula vista in precedenza, cambia direzione prima che cambi la pendenza. Infatti via via che arrivano nuove osservazioni nella nuova direzione. la pendenza inizia a variare, ma lo fa anche l’intercetta. Il coefficiente di correlazione si comporta in modo simile alla pendenza delle retta di regressione. Nei punti in cui la pendenza cambia segno la correlazione è pari a 0.
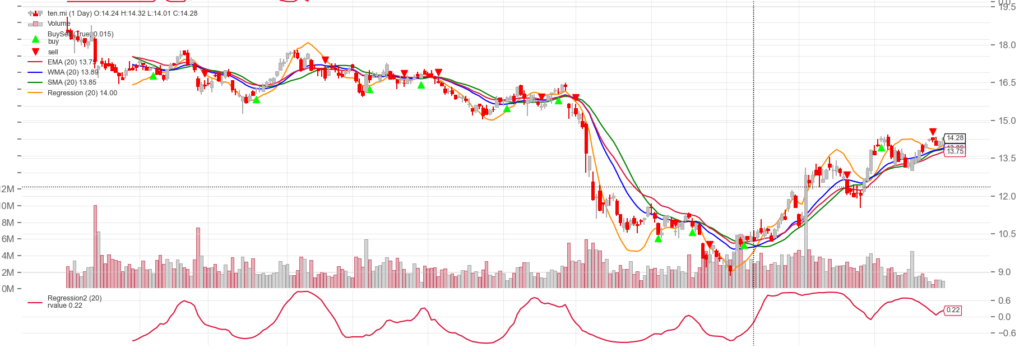
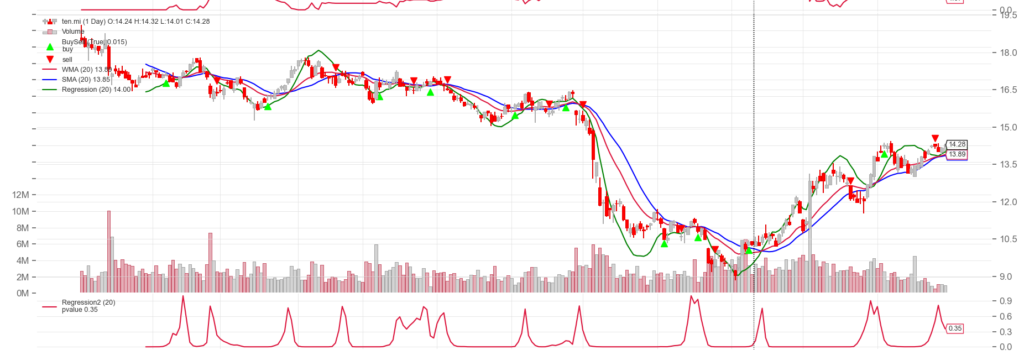
Il grafico a alato mostra il momento di cambio direzione su Tenaris nel periodo, si possono osservare un insieme di aumenti di prezzo, fortemente correlati, seguiti da un insieme di punti non correlati rispetto a quelli iniziali. Sia la pendenza delle rette, che il coefficiente di correlazione si stanno avvicinando allo 0.
Se la correlazione è minima nei punti in cui la retta cambia pendenza, il valore p diventa massimo. Rappresentando in un grafico il valore p-val, otteniamo evidenza della correlazione inversa tra r e p-val.
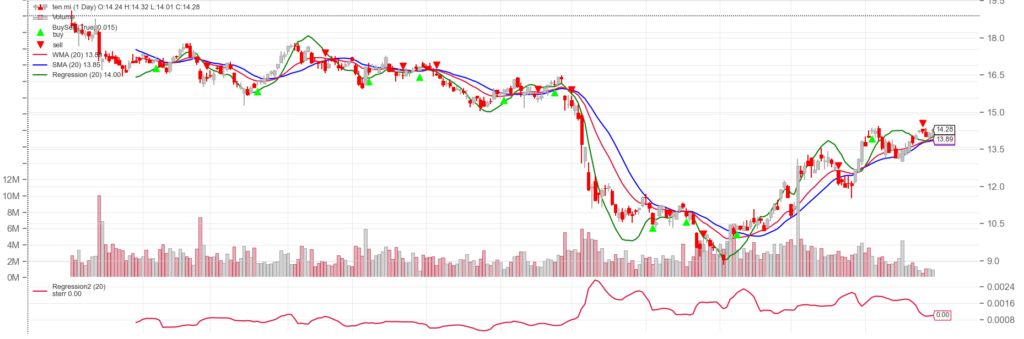
L’ultimo grafico riporta l’errore standard associato alla curva generata dalla regressione.
Conclusione
Utilizzare la regressione lineare al posto della media può avere un’applicazione pratica concreta per diversi fattori. Il più significativo è a mio avviso la possibilità di confrontare i valori di due diversi strumenti, questo può essere fatto tramite la pendenza della linea di regressione su scala logaritmica. La pendenza stessa può essere utilizzata come indicatore di momento, in modo analogo all’RSI. Potrebbe essere interessante applicare alcuni indicatori come MACD alla regressione lineare. O anche l’incrocio di medie mobili sfruttando la regressione lineare.

Lascia un commento